[C++] Quick Sort 퀵 정렬
[퀵 정렬의 이점]
- 무작위로 분포되어 있고, 많은 양의 데이터를 정렬할 때도 효율적이고 빠르다
- 메모리 요구량이 작음
- 보통의 경우의 정렬 효율은 Log N이지만 이미 정렬된 배열을 정렬하면 O(n^2) 효율이 되므로 주의해야 한다.
#include <iostream>
void swap(int &a, int &b);
void QuickSort(int *arr, int start, int end);
int main()
{
int qs[] = {7, 8, 5, 4, 3, 9, 1, 2, 6};
QuickSort(qs, 0, 8);
for (int i = 0; i < (int)(sizeof(qs) / sizeof(*qs)); i++)
{
std::cout << qs[i] << ",";
}
std::cout << std::endl;
}
void swap(int &a, int &b)
{
if (a == b)
return;
int temp = a;
a = b;
b = temp;
}
void QuickSort(int *arr, int start, int end)
{
if (start >= end)
return;
int &pivot = arr[start];
int i = start + 1;
int j = end;
while (i <= j) //(1)반복문
{
while (arr[i] < pivot && i <= end) //(2)반복문
{
i++;
}
while (arr[j] > pivot && j >= 0) //(3)반복문
{
j--;
}
if (i < j)
swap(arr[i], arr[j]);
else
break;
}
swap(pivot, arr[j]);
QuickSort(arr, start, j - 1);
QuickSort(arr, j + 1, end);
}[예제 배열의 순서가 바뀌는 과정]
main문에서 step1--QuickSort(arr, 0, 8)로 매개변수를 넘겨 주었으니

while (arr[i] < pivot && i <= end) // (2)반복문i는 pivot의 값보다 작고, end보다 작거나 같을 때 값을 증가시키며
while (arr[j] > pivot && j > 0) // (3)반복문j는 pivot의 값보다 크고, 0보다 클 때 값을 감소시킨다
(2), (3) 반복문이 종료된 결과는 i = 1, j=8이다
1---(2), (3) 반복문이 종료된 후
if (i < j)
swap(arr[i], arr[j]);
else
break;i는 1, j는 8, i < j가 참이므로 swap문에 진입하여 위치를 변경한다

(1) 반복문의 조건인 i <= j가 참이므로 반복하여 계산한다
2---(2), (3) 반복문이 실행된 후 결과는 i = 5, j =7이다

3--- (2), (3) 반복문이 실행된 후 결과는 i = 7, j =6이다
if( i < j)가 거짓이므로 (1) 반복문을 탈출한다
swap(pivot, arr[j]); // (swap(pivot, arr[6])탈출한 후 pivot과 arr[j]의 위치를 서로 바꾸어 준다.
(pivot은 arr[Start]의 레퍼런스이다.
int &pivot = arr[start];)

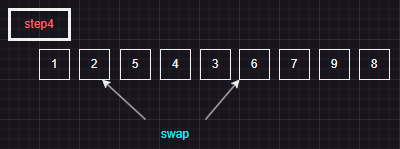
이후 step2--QuickSort(arr, start, j-1)문으로 진입한다
QuickSort(arr, start, j - 1); // start : 0, j - 1 : 5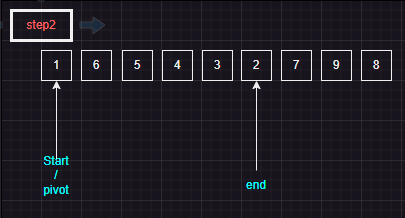
이전과 같이 (2), (3) 반복문을 계산하면 i = 1, j=0이므로 (1) 반복문을 탈출한다
이후 swap에서도 pivot의 값과 arr(j)의 값이 같으므로 순서의 변화는 없다
step3--QuickSort(arr, start, j-1)에서 j는 -1이되어 if(start >= end)문에서 return하게 된다.
step4--QuickSort(arr, j+1, end)
QuickSort(arr, j+1, end) // QuickSort(arr, 1, 5)로 진입하여 (2), (3) 반복문을 계산하면 i = 6, j = 5이므로 (1) 반복문을 탈출한다
swap(pivot, arr[j]); // swap(pivot, arr[5])의 결과는
step5-- QuickSort(arr, start, j-1)문으로 진입한다
이전과 같이 (2), (3) 반복문을 계산하면 i = 2, j=1이므로 (1) 반복문을 탈출한다
이후 swap에서도 pivot의 값과 arr(j)의 값이 같으므로 순서의 변화는 없다
step6-- QuickSort(arr, start, j-1)는 j가 0이므로 바로 함수를 종료한다
step7--QuickSort(arr, j+1, end)
QuickSort(arr, j+1, end); //QuickSort(arr, 2, 4)로 진입하여 (2), (3) 반복문을 계산하면 i = 5, j = 4이므로 (1) 반복문을 탈출한다
swap(pivot, arr[j]); // swap(pivot, arr[4])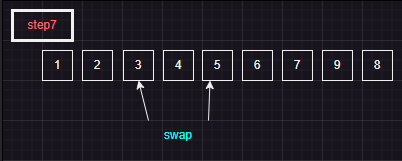
위와 같은 방식으로 따라가다 보면 자연스레 이해되는 것 같다
(모두 기록하려 했으나 귀찮아짐 ㅎ;)